Números enteros
Un numero entero es cualquier elemento del conjunto formado por los números naturales, sus opuestos (versiones negativas de los naturales) y el cero.
- Todos los números enteros mayores de cero se consideran positivos, y sus opuestos, se consideran negativos.
- El cero no es positivo, ni negativo, luego el opuesto del cero es el propio cero.
- El conjunto formado por el cero y todos los números enteros positivos, se denomina conjunto de los números enteros no negativos.
- El conjunto formado por el cero y todos los números enteros negativos, se denomina conjunto de los números enteros no positivos.
- Los números opuestos están situados en la recta numérica simétricamente respecto al cero.
- Los números enteros que solo se diferencian en el signo, se llaman opuestos, por ejemplo, 20 y -20 son números opuestos.
- El módulo o valor absoluto de cualquier número entero nunca es negativo. Dos números enteros opuestos tienen el mismo módulo, por ejemplo:
Representación de los números enteros sobre una recta
Se representan sobre una recta, llamada recta numérica, así:
El cero en mitad de la recta, los enteros negativos a la izquierda del cero y los enteros positivos a su derecha. Normalmente no se escribe el signo + que precede a los enteros positivos.
A continuación un resumen de los números enteros
Actividades

A) Realizar las siguientes operaciones con números enteros:
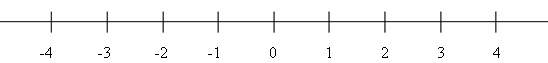
No hay comentarios:
Publicar un comentario